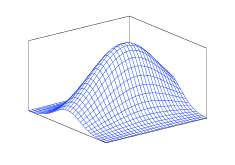
This post explains a few important properties of random variables. The first is joint probability of two random variables which is denoted as , or , which is short for . The joint probability of two random variables with normal probability distributions is shown in Figure 1. When the joint probability of two random variables is equal to the product of their probabilities individually, then the random variables are said to be independent, that is . The intuition behind this is that the value that takes on does not depends on the value that takes on, and it may be the case that the physical system which determines is not affected by the system which determines and vice versa. When a set of random variables are independent from each other and follow the same distribution we say they are independent and identically distributed (i.i.d.).
When and are dependent but do not occur together, we say they are mutually exclusive, or disjoint. Mutually exclusive random variables have the property that . The probability of or or both occurring is denoted as . For mutually exclusive random variables .
Often we want to make a prediction about the outcome of an experiment supposing that some event occurred, this is called conditional probability, and is denoted , in other words, the probability of given the occurrence of . Conditional probability is related to joint probability through the following formula
Independence between random variables can also be described by , that is, the probability of occurring given that has occurred is the same as the probability of occurring. When conditional probabilities are known we can describe the probability of a random variable in terms of its conditional probabilities. This is called marginalizing the probabilities. If we have probabilities for in the form of , the marginal probability of can be determined by summing the joint probabilities: , as long as partitions the probability space. That is, .