For background on probability systems, see my previous post. A random variable is really a function, called a measure function, from the sample space to the state space of a probability system. Like , a state space is a -algebra, typically the space of real numbers . In this case a random variable is defined as , for a probability space . The notation will be used as shorthand for the more explicit, well defined .
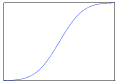
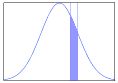
Any real-valued random variable (e.g. ) can be fully characterized by its cumulative distribution function. The cumulative distribution function, or CDF, is defined for a random variable as . If the CDF is a continuous function, then the random variable is said to be a continuous random variable. This type of CDF is illustrated in Figure 1. For a continuous random variable the probability of taking on any particular value is infinitesimally small (i.e. ), so we talk about the probability of the random variable taking on a value in a particular range instead, . The probability of a random variable taking on a value in a particular range is called the probability density, and is represented by the probability density function, , illustrated in Figure 2. Note that can be estimated by using a sufficiently small interval,
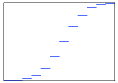
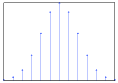
For discrete random variables, the variable takes on particular values over a discrete interval. We can define a function that represents the probability that is exactly equal so to some value , or . The CDF is a step function since increases in discrete steps as shown in Figure 3. The probability that takes on a particular value is given by the probability mass function, illustrated in Figure 4. Notice that the pmf is not continuous, .
3 thoughts on “Random Variables and Distributions”
Comments are closed.