In a previous article we discussed the idea of the convolution sum as a way to filter a signal when we know the desired impulse response. Convolution is a widely used technique in image processing to apply transformations to the signal. Since images are two-dimensional functions the impulse response is also two-dimensional, a matrix commonly called a kernel. Kernels often apply transformations to small neighborhoods of pixels, but as they are swept across the entire image the image as a whole is transformed. Figure 1 shows a one-dimensional convolution operation, while Figure 2 shows a two-dimensional convolution.
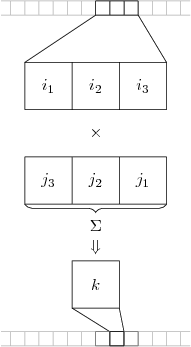
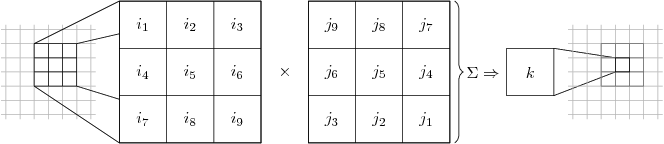
Here the values of represent the intensity values of the signal, while the values of represent the values of the kernel. Notice that the arrangement of the kernel values are reversed. Recall the formula for the convolution sum:
So the first value of the image neighborhood is multiplied with the last value of the kernel . The result of the convolution is the intensity value of the output signal at the center point of the neighborhood. To determine the output value at the convolution formula will take on the form .
In this way the kernel is “swept” across the image to determine the output value at each position. A problem arises when convolution is considered near the edges of the signal in a finite signal. For example, to determine the value of the convolution sum will require some values of which are not available (e.g., , etc) depending on the size of the kernel. What should be used in place of these values? There are several common approaches for dealing with this problem, called padding. The signal may be padded with enough zeros to satisfy the convolution sum, or the intensity values of the edge pixels may be replicated. Another approach is to mirror the pixel values about the edge, or to periodically repeat the pixel values. The resulting output signal will have a length of , where is the length of the input signal and is the length of the kernel. However, the only part of the output signal that is considered valid, that is does not contain padded values, the central part of the signal of length .
Cross-correlation is an operation similar to convolution, except it does not reverse the kernel when multiplying. Cross-correlation is often used to identify a the location of matching signals. A smaller signal is swept across a larger signal, when the signal is matched the values will be fully correlated resulting in maximal output.
One thought on “Convolution Transforms”
Comments are closed.