Vectors and Matrices

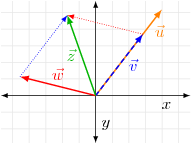
When we wish to express a quantity we use a number, however, many times it is useful to to describe ideas that are more complex than a single quantity, such as direction or a sequence. A vector is a mathematical structure consisting of an array of elements, typically written as , or , or simply when the type is made obvious by the context. Vectors represent a direction and magnitude or length, denoted . The vector of length zero is referred to as the zero vector, , while a vector of length one is called a unit vector. A vector can be arranged as a row or a column, here we will use row vectors in the interest of saving space when possible, such as . In this context a single quantity or number is referred to as a scalar. Vectors can represent a direction where each element, or component, specifies the contribution to the vector from the corresponding dimension. For example, in 2-dimensional space a vector may have 2 components, one specifying the contribution in the x-direction, the other for the y-direction. This is illustrated by the blue arrow in Figure 1. The blue vector in Figure 1 is defined by the vector . Vectors can be multiplied by a scalar to scale the vector along the same direction, that is, to change the magnitude of the vector, by scaling each component of the vector uniformly . For example the orange vector is a scaled version of the blue vector. Vectors can also be added together: the green vector is the sum of the blue and red vectors, .

The axes and are also vectors. Here they are a special set of vectors called the basis vectors or simply basis. Basis vectors are the vectors that define a space, or more accurately, a vector space. Any point in 2-dimensional space can be represented by an component and a component. In 1-dimensional space the real number line can be thought of as a basis vector, in 3-dimensional space the common , and axes are the basis vectors. In order for a set of vectors to fully describe a vector space they must be linearly independent. Linear independence means that for a set of vectors, none of the vectors in the set can be described by a linear combination (a sum of scaled vectors) of any of the others. For example, for the basis vectors in 3-dimensional space, none of vectors can be described by a combination of the other two. For a given basis any vector in the vector space can be represented as a linear combination of the basis vectors:

If a vector space is coupled with a structure called an inner product, the space is referred to as an inner product space. The inner product, denoted , maps a pair of vectors to a scalar value in a way that must satisfy the following axioms: , , , and , unless is the zero vector in which case . In Euclidian space, an inner product called the dot product is typically used. The dot product , or is equal to the sum of the pairwise products of the vector elements, . This gives a more rigorous definition for the length of a vector in Euclidean space using a function called a norm

The Euclidean distance between two vectors is determined using the dot product:

The dot product can also be used to find the angle between two vectors, given by:

The inner product provides the structure for the familiar concept of Euclidean space when combined with the vector space of real numbers. When the inner product of two non-zero vectors is equal to zero, the vectors are said to be orthogonal, sometimes expressed as . If each of the vectors is a unit vector as well, then they are said to be orthonormal. This can be expanded to a set of pairwise orthogonal or orthonormal vectors called an orthogonal set and orthonormal set, respectively.

A discrete random variable can be represented by a vector where each component of the vector represents the probability that the random variable is in an associated state. For example, a vector would indicate that the random variable has a 0.1 probability of being in state 1, a 0.3 probability of being in state 2, and so forth. With possible states the random variables represent -dimensional vectors in an -dimensional space.

A matrix extends the idea of a vector into multi-dimensional space. In some cases matrices only refer to 2-dimensional arrays with high dimensions being handled by tensors. Here we will refer to any array in more than one dimension as a matrix. A matrix is usually denoted in bold, as in , where the element or represents the element in the -th row and -th column, as shown in Figure 2. An matrix has rows and columns.

The matrix in Figure 2 is square because . The transpose of a matrix is the matrix mirrored along the diagonal, . If the transpose of a matrix is equal to the original matrix, it is called a symmetric matrix. The identity matrix is a special matrix whose element are all 0’s, except along the diagonal where they are 1’s:

An invertible matrix is one which has a multiplicative inverse such that . However, not all matrices are invertible. If a matrix is both square and invertible it is called non-singular.

A matrix represents a linear map; a homomorphism from one vector space to another vector space. The linear map is required to satisfy the linear property:

Alternatively, any linear function or first-degree polynomial in one variable of the form , where is a linear map. A linear map is equivalent to a matrix where and are -dimensional and -dimensional vector spaces, respectively, and applying the linear map to a vector is equivalent to multiplying by the matrix, called the linear transform. If the linear transform preserves the inner product, that is, the inner product between any two vectors is the same after the transform as before, then the transform is orthogonal.

Given a linear transform in the form of a matrix , an eigenvector is a non-zero vector which does not change in direction when the transform is applied, . Note that the vector may be scaled by a quantity , which is called the eigenvalue. Since the zero vector never changes direction under a linear transform it is a trivial case and normally excluded as an eigenvector.